Maple软件如何计算积分与极限
在数学的浩瀚海洋中,积分与极限是至关重要的概念,而maple软件则是处理这些问题的得力助手。它为我们提供了便捷高效的计算方法,让复杂的数学运算变得轻松简单。
积分计算
maple软件拥有强大的积分计算功能。对于不定积分,只需输入相应的函数,利用int命令就能快速得出结果。比如,求函数$f(x)=x^2+3x+1$的不定积分,在maple中输入int(x^2+3*x+1,x),瞬间就能得到$⁄frac{1}{3}x^3+⁄frac{3}{2}x^2+x+c$。
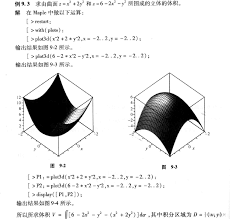
对于定积分,同样使用int命令,不过需要指定积分的上下限。例如,计算$⁄int_{1}^{2}(x^2+3x+1)dx$,输入int(x^2+3*x+1,x=1..2),就能迅速算出结果为$⁄frac{23}{6}$。
maple还能处理一些特殊函数的积分,像三角函数、指数函数等的复杂组合。它会依据相应的积分规则,给出准确的计算结果,大大节省了我们手动计算的时间和精力。
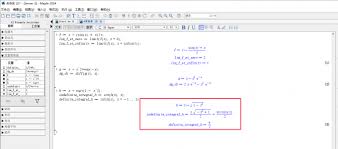
极限计算
在求极限方面,maple软件也表现出色。计算函数在某点的极限,使用limit命令。比如,求函数$f(x)=⁄frac{x^2 - 1}{x - 1}$在$x = 1$处的极限,输入limit((x^2 - 1)/(x - 1),x = 1),maple会立即给出极限值为2。
对于更复杂的极限问题,如$⁄lim_{x ⁄to ⁄infty} ⁄frac{3x^3 + 2x^2 + 1}{2x^3 - 5x + 2}$,输入limit((3*x^3+2*x^2+1)/(2*x^3 - 5*x + 2),x = infinity),就能得到极限值为$⁄frac{3}{2}$。
maple软件不仅能计算常规的极限,对于一些带有参数的极限问题也能很好地解决。它会根据参数的不同取值情况,给出准确的极限结果,为我们深入研究函数的性质提供了有力支持。
总之,maple软件在积分与极限的计算上具有显著优势,无论是简单的函数还是复杂的数学表达式,它都能快速准确地给出结果。掌握maple软件的这些计算方法,能让我们在数学学习和研究中事半功倍,畅游在数学的奇妙世界里。









